Assertion Predicates (previously known as "Skeleton Predicates")
Assertion Predicates1 are a specific kind of predicates found in the C2 compiler that accompany Hoisted Check Predicates created during Loop Predication. Their only purpose is to make sure that the C2 IR is in a consistent state. Compared to Hoisted Check Predicates, they do not represent a required check that needs to be executed during runtime to ensure correctness. They could be removed after the loop optimization phases - hence the name “Assertion Predicates”. But if Assertion Predicates are not required at runtime, why do we need them anyway? The reason is found in the very nature of the C2 IR.
There are other kinds of predicates which I will not cover in this blog article but possibly in a future one.
Background
Sea of Nodes
The IR combines data and control flow into a single representation which is known as sea of nodes2 . This has a couple of implications - one of them is that data and control always need to be in sync.
Control and Data Are Always in Sync
If at some point a control path is proven to be never taken, we not only need to remove the control nodes but also the data nodes specific to that path. The same principle is also true when data nodes die: If a data node dies within a specific path, then all control nodes using this data node directly or indirectly must become unreachable. The path containing these nodes needs to be removed. While the first property is not that difficult to maintain (data nodes without uses are just removed), the latter is not that straight forward. We need to completely remove all control nodes on the current path with the same or higher nesting level as the dead data. Let’s illustrate this with a simple example:
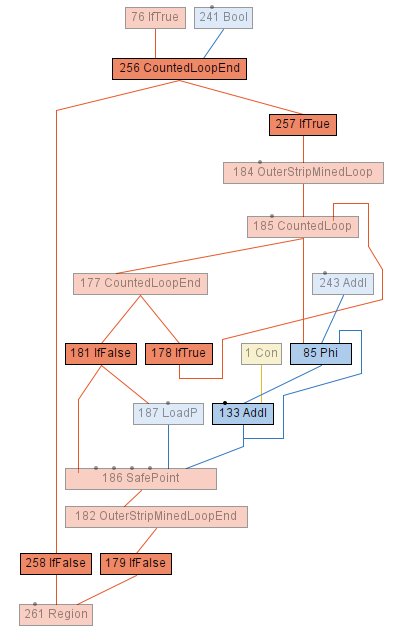
Here we have a counted loop 185 CountedLoop/177 CountedLoopEnd inside which the data node 133 AddI is dying (top
input 1 Con). The loop phi 85 Phi uses this dead data node and is therefore also considered dead. Since there is no
other control flow inside the loop, we need to make sure that the entire loop becomes unreachable (same nesting level
as 133 AddI). We can achieve that by ensuring that the condition 241 Bool of the zero-trip guard
256 CountedLoopEnd3, which is at a lower nesting level than 133 AddI, becomes false. As a
result, we will always take the path of 258 IfFalse and the graph is consistent again.
Failing to keep control and data in sync can have unpredictable consequences in further optimizations and code emission. We could end up hitting an assertion failure further down the road or emitting wrong code, resulting in a crash or wrong execution at runtime.
With that in mind, let’s first look at Loop Predication to better understand the need for Assertion Predicates.
Loop Predication
The goal of Loop Predication is to hoist certain checks out of a loop. As a result, we only need to execute these checks once before the start of the loop instead of during each iteration which has a positive impact on performance.
Conditions
Loop Predication can only remove checks (i.e. a IfNode/RangeCheckNode) out of a loop if they have an uncommon trap
on one path and if they belong to one of the following category:
- The check is loop-invariant (e.g. null checks of objects created outside the loop).
- The check is a range check (i.e. either a
RangeCheckNodeor anIfNode4) of the formi*scale + offset <u array_length, whereiis the induction variable,scaleandoffsetare loop-invariant,array_lengthis the length of an array (i.e. aLoadRangeNodeor a constant), and the loop is a counted loop (i.e. represented by aCountedLoopNodeinside the IR).
Why Do Array Range Checks Have a Single Unsigned Comparison?
For an array, we need to check that the index is zero or positive and strictly less than the size of the array:
i*scale + offset >= 0i*scale + offset < array_length
This means that we would need two checks for each array access. But we can combine them into a single check by using
the following unsigned comparison trick (converting i*scale + offset and array_length to unsigned and do the
comparison):
i*scale + offset <u array_length
Let’s see what happens when we convert i*scale + offset to unsigned:
- If
i*scale + offset < 0: Convertingi+scale + offsetto unsigned results in an integer greater thanMAX_INTand therefore greater thanarray_lengthwhich is at mostMAX_INT:MAX_UINT >= (unsigned)(i*scale + offset) > MAX_INT >= array_lengthThe unsigned comparison will therefore fail.
- If
i*scale + offset >= array_size: The check just fails as it would have if it had been a signed comparison.
Hoisting Invariant Checks
Once we find a check that qualifies to be hoisted out of a loop, we move it right before the loop. This is straight forward for invariant checks, where we can simply re-use the condition inside the loop as a condition for the check outside the loop.
One Hoisted Check Predicate
We therefore create a single Hoisted Check Predicate for a loop-invariant check before the loop and kill the old check inside the loop.
Hoisting Range Checks
Range checks are a little bit trickier as we need to cover the index check i*scale + offset <u array_length for all
possible values of the induction variable i. Since scale and offset are loop-invariant, and we have a counted
loop, we actually only need to perform the index check for the initial value of i (i.e. init) and the value of
i in the last iteration (i.e. last), assuming a stride stride and a loop limit limit (i.e. the loop looks like
for (int i = init; i < limit; i += stride)):
init*scale + offset <u array_lengthlast*scale + offset = (limit-stride)*scale + offset <u array_length
Two Hoisted Check Predicates
We therefore create two Hoisted Check Predicates for a range check before the counted loop: One with inserting the
initial value of the induction variable and one with inserting the value of the induction variable in the last iteration
for the index check i*scale + offset <u array_length. The old range check inside the loop is removed.
What Happens if a Hoisted Check Predicate Fails at Runtime
If a Hoisted Check Predicate fails at runtime, we trap and simply jump back to the interpreter and continue execution right before the loop. Since Hoisted Check Predicates are evaluated once before the start of the loop, we have not executed any iteration of the loop, yet. It is therefore safe to resume execution in this way.
Now that we’ve recapped on how Loop Predication works, we can have a closer look at why this simple idea of creating Hoisted Check Predicates introduces a new fundamental problem for the C2 IR.
A Fundamental Issue with Hoisted Check Predicates for Range Checks
Regardless on how we further optimize a loop (peeling, unrolling, unswitching etc.), if a Hoisted Check Predicate for a loop fails, we will always trap before executing any iteration and resume in the interpreter just before the start of the loop. However, when splitting such a loop into sub-loops, we could run into a fundamental problem for Hoisted Check Predicates created for range checks due to the mixture of control and data in the C2 IR.
Let’s work through an example to illustrate why.
Loop Predication Example to Hoist a Range Check
Let’s have a look at the following example, assuming that limit is a field from which C2 does not know anything
about (i.e. its type is just #int):
for (int i = 1; i > limit; i -= 2) {
a[i] = 34;
}
C2 emits a RangeCheckNode for the array access a[i]:
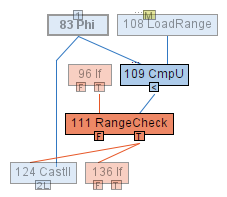
83 Phi is the induction variable i and 108 LoadRange the size of the array. C2 knows that the type of 83 Phi
is [min+1..1] because we start at the initial value i = 1, the stride is -2, and limit could be anything (i.e.
worst case MIN_INT and thus i cannot get smaller than MIN_INT + 1). We know, by design, that after performing any
range check, an array index i will always satisfy 0 <= i < MAX_INT. On top of that, we can improve the upper bound
of the index by taking the maximum value of i that we know from the type of 83 Phi. We therefore insert an
additional 124 CastII to store the improved type [0..1] for the array index at a[i].
Loop Predication will identify 111 RangeCheck as valid range check and remove it from the loop by creating two
Hoisted Check Predicates. We will denote the Hoisted Check Predicates with PU(a[i]), for the upper bound, and
PL(a[i]), for the lower bound:
// Check: init*scale + offset <u array_length`
// <=> 1*1 + 0 <u a.length
// <=> 1 <u a.length
PU(a[i])
// Check: (limit-stride)*scale + offset <u array_length
// <=> (limit-(-2))*1 + 0 <u a.length
// <=> limit+2 <u a.length
PL(a[i])
for (int i = 1; i > limit; i -= 2) {
a[i] = 34;
}
So far, so good.
Splitting the Loop into Sub-Loops where One of Them Is Dead
Now let’s assume that we apply Loop Peeling for the loop in our example5. Loop Peeling splits the first iteration from the loop to execute it before the remainder of the loop. We can do that by cloning the loop and changing the bounds in such a way that it only runs for one iteration. We are therefore left with two sub-loops: The first runs for a single iteration and the second runs for the remaining iterations:
// Check: init*scale + offset <u array_length`
// <=> 1*1 + 0 <u a.length
// <=> 1 <u a.length
PU(a[i])
// Check: (limit-stride)*scale + offset <u array_length
// <=> (limit-(-2))*1 + 0 <u a.length
// <=> limit+2 <u a.length
PL(a[i])
// Peeled iteration
for (int i = 1; i > -1; i -= 2) {
a[i] = 34;
}
// Remaining loop
for (int i = -1; i > limit; i -= 2) {
a[i] = 34;
}
The first loop is not a real loop anymore as we are never taking the backedge. IGVN6 will therefore fold this single loop iteration into a simple sequence of statements, achieving the goal of Loop Peeling:
// Check: init*scale + offset <u array_length`
// <=> 1*1 + 0 <u a.length
// <=> 1 <u a.length
PU(a[i])
// Check: (limit-stride)*scale + offset <u array_length
// <=> (limit-(-2))*1 + 0 <u a.length
// <=> limit+2 <u a.length
PL(a[i])
// Peeled iteration
a[1] = 34;
// Remaining loop
for (int i = -1; i > limit; i -= 2) {
// Type of iv phi i [min+1..-1]
a[CastII(i)] = 34;
}
IGVN will also update types, including the types of the induction variable 83 Phi and array index 124 CastII.
83 Phi will use the new initial value of the induction variable, -1, and update its type to [min+1..-1]
accordingly. This type is propagated to its output 124 CastII which computes its own new type (see CastII::Value())
by taking this input type and joining it with the type it casts to (i.e.[0..1]). But these two type ranges do not
overlap! In such a case, we set top as type - meaning an empty set of possible values. IGVN will then replace the
entire CastII node with the dedicated top node.
Propagating Top to All Uses of the CastII Node
IGVN will do its work and propagate top to all uses of the CastII node - possibly converting these nodes to
top as well. This triggers a cascade of removals which is only stopped at nodes which can handle top in such a
way that the node itself does not die (e.g. a PhiNode which merges multiple values from different paths).
The Remaining Loop Is Dead Anyway - Where Is the Problem Now?
You might argue now while looking at the code after Loop Peeling that the remaining loop, starting at -1, will never
be executed. This is true because if limit < 0, then the Hoisted Check Predicate will fail at runtime and we trap. If
limit >= 0, then the loop will not be entered. Either way, the loop is never executed and evidently dead. So why
don’t we just remove it and go home? Well, yes, but how?
Won’t the Replacement of the CastII Node with Top Kill the Dead Sub-Loop?
Unfortunately, no, it will not. Let us remind us of the fundamental IR graph property that data and control always need
to be in sync. If data in one path dies, this control path needs to be removed as well - but that is not automatically
happening! Even though the loop is evidently dead at runtime, C2 does not know that. There is no IfNode or anything
alike that would take care of removing the remaining dead sub-loop after peeling. The graph is left in an inconsistent
state: Some data/control/memory nodes could have been removed while others still remain inside the dead loop. This
could lead to assertion failures even though any of the not yet cleared nodes inside this dead sub-loop will never be
executed at runtime.
CastII Nodes Are Updated - Hoisted Check Predicates Are Not
How did we end up in this situation? The problem is that each time we are updating the initial value of the induction
variable, the stride and/or the limit of the loop, the involved CastII node for the array index (and potentially
other CastConstraint nodes dependent on the induction variable, stride and/or limit) are updated while Hoisted
Check Predicates are not. If a Hoisted Check Predicate cannot be proven to always fail, then we still cannot prove it
after splitting the loop in an arbitrary way (assuming that we will not find out anything new about the loop in the
meantime).
How Can We Fix This?
How can this discrepancy between CastConstraint nodes and Hoisted Check Predicates be prevented? How can we ensure a
dead sub-loop is cleaned up when data is dying inside it? How can we establish the synchronization of control and data
again? The answer lies within Assertion Predicates.
Assertion Predicates
Now that we understand the fundamental issue with Hoisted Check Predicates, we need to address it. Our solution is to set up a special version of each Hoisted Check Predicate for each sub-loop such that it reflects any new initial value of the induction variable, new stride, and new limit. We call these versions Assertion Predicates.
Fold Dead Sub-Loop Away
Having these additional Assertion Predicates in place will now take care of folding dead sub-loops away. Let’s revisit
our example from the last section and see how we can create Assertion Predicates AU and AL as special versions
of the Hoisted Check Predicates PU and PL when peeling a loop:
// Check: init*scale + offset <u array_length`
// <=> 1*1 + 0 <u a.length
// <=> 1 <u a.length
PU(a[i])
// Check: (limit-stride)*scale + offset <u array_length
// <=> (limit-(-2))*1 + 0 <u a.length
// <=> limit+2 <u a.length
PL(a[i])
// Peeled iteration
a[1] = 34;
// Remaining loop
// Two Assertion Predicates - updated version of PU and PL above
// Check: init*scale + offset <u array_length`
// <=> -1*1 + 0 <u a.length
// <=> -1 <u a.length
AU(a[i])
// Check: (limit-stride)*scale + offset <u array_length
// <=> (limit-(-2))*1 + 0 <u a.length
// <=> limit+2 <u a.length (Same as PL because stride and limit are the same)
AL(a[i])
for (int i = -1; i > -1; i -= 2) {
a[i] = 34;
}
We can immediately see that AU compares -1 <u a.length which, obviously, always fails. We would therefore never
enter the loop. Accordingly, IGVN is now able to safely remove the created dead sub-loop and its involved data. The
graph is consistent again7.
Always True at Runtime
An Assertion Predicate will always be true during runtime because it re-checks something we’ve already covered with
a Hoisted Check Predicate. We can therefore completely remove an Assertion Predicate once loop optimizations are over.
But for debugging purpose, it helps to keep these Assertion Predicates alive to ensure that none of these will ever fail.
To do that, we implement the failing path with a HaltNode instead of a trap. Executing the HaltNode at runtime will
result in a crash.
Always Added/Updated when Modifying the Initial Value of an Induction Variable, the Stride or the Limit of a Loop
We always insert Assertion Predicates when changing a loop, for which we created Hoisted Check Predicates, in such a way that either the initial value of the induction variable, the stride, or the limit is updated. This happens when:
- Peeling a Loop:
- The remaining loop needs Assertion Predicates.
- Creating Pre/Main/Post Loops:
- The main and post loop need Assertion Predicates.
Furthermore, we need to update existing Assertion Predicates when:
- Unrolling a Main Loop:
- The main loop Assertion Predicates need to be updated because we change the stride.
- Unswitching a Loop:
- The fast and the slow loop need a version of the Assertion Predicate (we could split these loops further).
There is one more case where we need to insert Assertion Predicates even though we have not created any Hoisted Check Predicate:
- Range Check Elimination:
- The pre and main loop bounds are updated such that a range check inside the main loop can be removed. This is similar to Loop Predication but instead of creating a Hoisted Check Predicate, we change the iterations of the pre and the main loop. The consequence, however, is the same: We need Assertion Predicates for the main loop to keep the graph in a consistent state if the main loop becomes dead8.
Implementation Attempts
Even though Loop Predication has been around for quite a while9, this problem was only
detected years later. At that time, the scope of the problem was not yet entirely clear. We’ve started adding
Assertion Predicates (back then known as Skeleton Predicates) for different loop optimizations as new
failing testcases emerged. Over the time, more and more CastConstraint nodes were added which made the still
very uncommon case more likely - especially with more enhanced fuzzer testing.
What had started out as a simple, clean fix (relatively speaking), when Skeleton Predicates were first introduced in JDK-8193130, became much more complex with each new fix. The latest bigger fix, at the time of this writing, was to add Assertion Predicates at Loop Peeling10. And yet, even though we now cover all loop optimizations, there are still cases which we do not cover properly when combining different loop optimizations together. The code became very complex and difficult to maintain over the years and fixing these cases became nearly impossible.
Cleaning up Predicates and Fixing Assertion Predicates
On top of these problems with Assertion Predicates, we have other kinds of predicates in the C2 code which we did not properly name. This made talking about “predicates” even more confusing as we’ve lacked a clear naming scheme. All of that led us to come to the conclusion that it’s time to bring order into the C2 predicates. We wanted:
- A clear naming scheme of predicates
- Cleaning up the predicate code (i.e. variable and method names, predicate matching code, comments, unifying and grouping methods to skip over predicates together etc.)
- Redesigning Assertion Predicates to fix the remaining issues
The first two goals are prerequisites to make the redesign of Assertion Predicates simpler and only even possible in a clean way.
Conclusion
We’ve discussed a long-standing issues with Hoisted Check Predicates and how this was attempted to be fixed over the last years with Assertion Predicates. A complete solution is yet to be added. However, we’ve filed JDK-8288981 with its sub-tasks to achieve this. Over the last months, I’ve shifted my focus towards achieving this goal. The cleanup and re-implementation of Assertion Predicates is almost done as of today. The only major thing left is to clean up the code further and heavily test my patches to ensure correctness.
I’ve written this blog post mainly to give an introduction into Assertion Predicates but also to ease the review process of my patches - at least on a high level. A potential follow-up blog post should cover the remaining predicates and how they are used within C2.
1Before the overall predicate renaming, Assertion Predicates have been known as Skeleton Predicates.
2Also see A Simple Graph-Based Intermediate Representation.
3In this example, we’ve peeled an iteration of the loop to establish a zero-trip
guard. Therefore, we have a CountedLoopEndNode and not a normal IfNode.
4Almost always, a range check will be a RangeCheckNode as it is unusual to write
code that would emit an IfNode with an unsigned comparison with a LoadRangeNode or a constant, a trap on the
uncommon path, and satisfying all other conditions to qualify for being hoisted as a range check out of a counted loop.
5Loop Peeling would not actually be triggered for this example as there is no reason to peel (see IdealLoopTree::estimate_peeling()). But for the sake of simplicity, let’s assume that C2 actually applies Loop Peeling for this example.
6 Short for Iterative Global Value Numbering. In the context of C2, Global Value Numbering tries to replace an IR node with another one that computes the same result. This could either be an existing IR node with the same hash (i.e. shares the same inputs) or a new IR node that does the computation in a more optimized or canonical way. Iterative Global Value Numbering applies this technique iteratively to a set of IR nodes until a fixed-point is reached. More information about Global Value Numbering in C2 can be found here.
7The careful reader might ask now how we can prevent to accidentally remove the entire remaining graph when folding an Assertion Predicate away? C2 actually establishes a dedicated zero-trip guard which checks beforehand if the remaining loop should be entered depending on the induction variable and the limit. We put the Assertion Predicates right into the “enter the loop”-path of the zero-trip guard check. Since we would never enter the dead-sub loop, Assertion Predicates will only kill the dead sub-loop inside the “enter the loop”-path. Note that a zero-trip guard and an Assertion Predicate are not the same. The former checks the induction variable against the loop limit while the latter compares it against the array length. Let’s see how our example actually looks like with the dedicated zero-trip guard after peeling the loop:
// Check: init*scale + offset <u array_length`
// <=> 1*1 + 0 <u a.length
// <=> 1 <u a.length
PU(a[i])
// Check: (limit-stride)*scale + offset <u array_length
// <=> (limit-(-2))*1 + 0 <u a.length
// <=> limit+2 <u a.length
PL(a[i])
// Peeled iteration
a[1] = 34;
// Remaining loop
// Zero-trip guard
if (i > limit) {
// Two Assertion Predicates - updated version of PU and PL above
// Check: init*scale + offset <u array_length`
// <=> -1*1 + 0 <u a.length
// <=> -1 <u a.length
AU(a[i])
// Check: (limit-stride)*scale + offset <u array_length
// <=> (limit-(-2))*1 + 0 <u a.length
// <=> limit+2 <u a.length (Same as PL because stride and limit are the same)
AL(a[i])
// The IR uses a do-while structure
do {
a[i] = 34;
i -= 2;
while (i > -1);
}
8Loop Predication and Range Check Elimination achieve the same goal to remove range checks from loops. Most of them can be removed with Loop Predication. But there are some cases where we cannot apply Loop Predication anymore (e.g. we’ve lost the Parse Predicates which provide the required safepoint for the Hoisted Check Predicate trap) while Range Check Elimination is still possible. More information about Range Check Elimination can be found here.
9First version added with JDK-6894778.
10See JDK-8283466.
Disclaimer: All the information provided in my blog posts reflects my point of view - use everything with care. My goal is to give easily understandable introductions, overviews, guidances, and/or learning opportunities - for you and me. To achieve that, I aim for simplicity and focus on ideas, rather than getting lost in details to get absolute completeness. This means that I sometimes omit implementation specific details to keep things simple and more general. The truth will always be found in the actual code. Keep in mind that, generally, anything mentioned in my blog posts could potentially be subject to change at any point.